NOTE: the data used comes from the coronavirus.politologue.com website.
Brief reminder on modeling
To model is to propose a representation of reality, in order to simulate the behavior of a system. The results of a model, however relevant it may be, will therefore only be an approximation of the truth. We can schematically identify three categories of models: empirical, analytical and numerical models:
- Empirical models do not seek to describe the underlying physics of a phenomenon, but aim to give a mathematical expression that describes existing results or observables as well as possible,
- In an analytical approach, the modeler establishes relevant equations (i.e. those that make sense in relation to the phenomenon being studied) and tries to solve them, at the cost of approximations and controlled hypotheses, and with a view to reducing calculation time,
- When the system of equations is too complex to solve directly, or when one does not wish to proceed to reductive approximations, the use of a numerical approach is necessary. This then requires the use of specific solvers (solving techniques).
Empirical models require a large experimental data set, but a low computing power. Their extrapolation outside the calibration domain is not legitimate. On the other hand, numerical models (or codes), especially multi-dimensional ones, can require very large computational resources but are often usable ab initio and for a wide range of applications (fluid mechanics, thermics, etc.).
The above is extremely simplified (one could point out, for example, that numerical models are themselves based on empirical or analytical sub-models: equations of state, laws of rheological behaviour, etc.), but will enable us to better understand certain characteristics of epidemiological models.
Our first empirical model
If we look at the evolution of the number of COVID-19 cases identified in France, the most adequate empirical representation presents an exponential form, which can be expressed as:
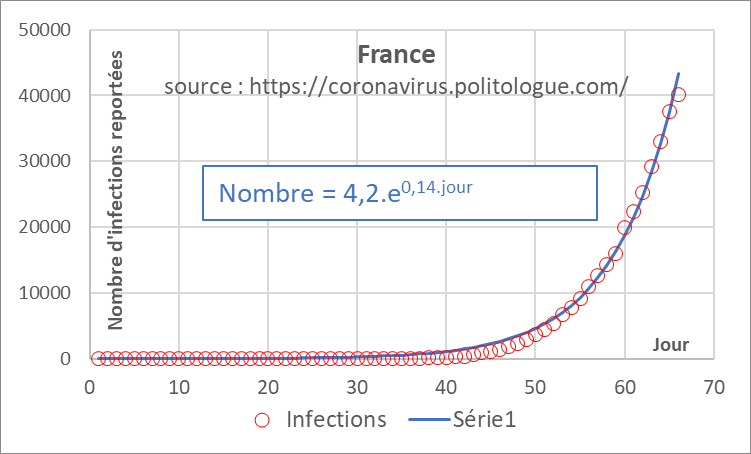
The limits of this representation are obvious, in particular the fact that the number of cases is rapidly tending towards infinity while the French population is about 67 million individuals (a number that reached 118.5 on day 118.5, around May 20). Its predictive interest is very limited: one cannot describe a priori the effect of measures aimed at containing the epidemic. Finally, and even if the representation seems adequate, the parameters used have no apparent physical meaning.
Mathematical Epidemiology
The simplest epidemiological models are “compartmentalized” (analytical) models, in which the population is divided into groups representing the development of the epidemic. One of the simplest models is the SIR (Susceptible, Infected, Recovered) three-compartment model, to which we will return in detail in a future article, and which allows us to trace the exponential evolution of the number of infected persons at the beginning of the epidemic.
Compartmental models are based on the assumption of a homogeneous population (no spatial dimension) and are generally solved in a deterministic way. Their mathematical description is based on a set of ordinary differential equations (ODEs) that describe the flows between compartments. These models have few parameters and the computational load is very low. However, their use is more frequently retrospective (to explain epidemics that have already ended) than predictive, because many phenomena (mobility, human behaviour, medical and non-medical countermeasures…) cannot be taken into account. Moreover, the intrinsically stochastic nature of the problem makes it difficult to estimate parameters during the course of an epidemic.
To overcome these problems, many variants of compartmentalized models have been proposed: taking into account new compartments, mobility, meta-populations, contact networks; stochastic resolution, etc. These modifications inevitably increase the number of parameters to be set…
At the other end of the complexity spectrum are agent-based models, which can be assimilated to numerical models of epidemiology. Agents” represent individuals or groups of individuals with similar characteristics. This approach makes it possible to take into account complex behaviours (categories of people, realistic mobility, contact rates that vary with time, influence of age, etc.). In return for this finesse of representation, agent-based approaches require the identification of tens or hundreds of parameters, and the calculation time is high (hours or even days).
About mobility…
Mobility modelling is an important (and underestimated) sub-problem of mathematical epidemiology. However, the current situation shows a strong spatial heterogeneity (cf. map below from https://coronavirus.politologue.com/carte-de-france/), and cell phone data are able to trace for example the “flight” of more than one million people from the Ile de France region to the province between March 13 and 20 (https://www.lemonde.fr/pixels/article/2020/03/26/confinement-plus-d-un-million-de-franciliens-ont-quitte-la-region-parisienne-en-une-semaine_6034568_4408996.html).

Globally, air transport has been a key vector for importing Coronavirus from China, and is likely to be a key vector for future emergences. To illustrate the difficulty of any prediction, researchers at INSERM (French National Institute for Health and Medical Research) estimated on January 24 using the GLEAM (Global epidemic and mobility model, https://www.gleamviz.org/) that the risk of importing the epidemic into France by air was 5% to 13%, an estimate that was subsequently modified on January 30. At the same time, it was thought “very unlikely” that a large-scale epidemic would develop in France .
If I quote this, it is not to throw the stone to these researchers, who had the courage to publish first predictions, but to show, by being a modeler myself, that the modeling of complex phenomena is far from being an exact science. As Cicero, taking up Cato again, already said: “Two augurs cannot look at each other without laughing.
As with mathematical epidemiology, models of human mobility vary from the simplest (no mobility) to the most complex (here again, agent-based models, such as those used for example to study evacuations on the scale of a city in the ANR ESCAPE project – Eric Daudé). Empirical intermediate models can be based on telephone data (difficult to extrapolate from one area to another) or on simple mathematical relationships that have proven their effectiveness (for example, according to the Lévy distribution, the probability of a displacement of length l is proportional to 1/l²).
Promising research is underway to “make sense” of travel patterns, for example the determination of “daily routines” (taking children to school, going to work, etc.) and could be further improved by taking into account real geolocalized points of interest and by exploiting statistical surveys (e.g. the CEREMA certified mobility surveys, or EMC²: https://www.cerema.fr/fr/activites/mobilite-transport/connaissance-modelisation-evaluation-mobilite/observation-analyse-mobilite/enquetes-mobilite-emc2, or the INSEE’s mobility survey of people: https://www.insee.fr/fr/information/3365007).
Last but not least: human behavior
Daily information shows us that individual or group behavior plays a major role: “rush” towards essential foodstuffs when the containment is announced, escape from supposedly high-risk areas, disregard by some of the containment instructions, etc. These behaviors are more strongly country-dependent, as shown for example by a recent study on immunization (https://wellcome.ac.uk/reports/wellcome-global-monitor/2018): in France, the most skeptical country, 19% of respondents believe that vaccines are not effective and 33% that they are not safe; the respective figures in Germany are only 3% and 13%.
Behavioural models fall into two broad categories: rules-based models and cost-benefit models. As their name suggests, the former model human behavior through a set of deterministic or stochastic rules. The latter, derived from game theory, postulate that human behaviour aims to maximize a utility (or gain) function whose expression can be very complex. An Armament Engineer General who lectured at ENSIETA spoke of “minimizing its annoyance function”, which of course comes down to the same thing… The difficulty with models based on game theory is the parameterization of the utility function, and in particular the quantification of non-economic “costs” (the “cost” of reducing our social relations, the “cost” of being infected by the coronavirus, etc.).
It should also be mentioned that human behaviour is influenced by the positive or negative information present on the various communication networks. The spread of “fake news” or “infox” can be modelled by epidemiological models…
To go further
As one can imagine, there is no shortage of resources on mathematical epidemiological models these days. A few scientific articles are proposed below, but they constitute only a tiny part of the information available.
I will continue this series in a few days with a more detailed article on the SIR compartmentalized model, but for now I’m going back to teleworking! In the meantime, stay at home, take care of yourself and your family, help the needy, and don’t underestimate the seriousness of the situation…
References
Allen L.J.S. ; “A primer on stochastic epidemic models : Formulation, simulation numérique et analyse” ; Infect. Disease Model, 2, 128-142 ; (2017).
Area Y. et al. ; “On a fractional order Ebola epidemic model” ; Advances in Diff. Equations, 2015:278 (2015).
Arino J. et van den Diessche P. ; “Disease Spread in Metapopulations” ; Fields Institute Communication ; (2006).
Balcan D. et al, “Multiscale mobility networks and the spatial spreading of infectious diseases” ; PNAS 22 décembre 2009 106 (51), 21484-21489 ; (2009).
Bichara D. ; ” Étude de modèles épidémiologiques : Stabilité, observation et estimation de paramètres. ” ; Thèse de doctorat ; Université de Lorraine ; (2013)
Bilge, A.H., Samanlioglu, F. & Ergonul, O. ; “On the uniqueness of epidemic models fitting a normalized curve of removed individuals” ; J. Math. Biol. 71, 767-794 (2015)
Brauer F. ; “Mathematical epidemiology : passé, présent et futur” ; “Modélisation des maladies infectieuses”, 2, 113-127 ; (2017)
Castillo-Chavez C. et al ; “Perspectives sur le rôle de la mobilité, du comportement et des échelles de temps dans la propagation des maladies” ; Proc Natl Acad. Sci USA, 113 (51), 14582-14588, (2016).
Chowell G. ; “The basic reproduction number R0 and effectiveness of reactive interventions during dengue epidemics” ; Math. Biosciences et ingénierie, 10 (5&6), 1455-1474, (2013)
Colizza V. et al ; “The role of the airline transportation network in the prediction and predictability of global epidemics” ; PNAS 14 février 2006, 103 (7), 2015-2020 ; (2006)
Cooley P. et al ; “The Role of Subway Travel in an Influenza Epidemic : A NYC Simulation” ; J. of Urban Health : Bulletin of the NY Academy of Medicine, Vol. 88, No. 5 ; (2011)
Daudé E., Eliot E. ; ” Exploration de l’effet des types de mobilités sur la diffusion des épidemies ” ; Septièmes Rencontres de Théo Quant, (2005).
Enduri M.K. et Jolad S. ; “Dynamics of Dengue with Human and Vector Mobility” ; Quantitative Biology – Polulation an d Evolution ; arXiv:1409.0965 [q-bio.PE] ; (2015)
Commission européenne ; “Statistiques comparables sur l’emploi du temps – Tableaux nationaux pour 10 pays européens” ; ISBN 92-894-8553-1 ; (2005)
Favro K. et Favro-Sabatier F. ; ” Comment limiter le risque infectieux du personnel médical ? ” ; Revue générale de droit médical, n°16, p.135 ; (2005).
Favro K. et Zolynski C. ; ” De la régulation des contenus haineux à la régulation des contenus (illicites) ” ; à paraître, Légipresse.
Finger F. et al ; “Mobile phone data highlights the role of mass gatherings in the spreading of cholera outbreaks” ; Proc Natl Acad. Sci USA, 113 (23), 6421-6426 ; (2016)
González M., Hidalgo C.A. et Barabási A.-L. ; “Understanding individual human mobility patterns” ; Nature 453, 779-782 ; (2008)
Hunter E. et al ; “A Comparison of Agent-Based and Equation Based Models for Infectious Disease Epidemiology” ; in Proc. of the Irish Conf. on AI and Cognitive Science ; (2018)
Kermack W.O. et McKendrick A.G. ; “A contribution to the Mathematical Theory of Epidemics” ; Proc. R. Soc. Lond. A, 115 ; p. 700-721 ; (1927)
Maneerat S., Daudé E. ; “A spatial agent-based simulation model of the dengue vector to explore its population dynamics in urban areas” ; Ecological Modelling, 333, 66-78, (2016).
Mi Ondo J.M. ; ” Les aspects spatiaux dans la modélisation en épidémiologie ” ; thèse de doctorat ; Médecine humaine et pathologie ; Université de Grenoble ; (2012).
Osthus D. et al ; ” Forecasting seasonal influenza with a state-space SIR model ” ; Ann Appl Stat. 2017 March ; 11(1) : 202-224, (2017)
Reluga T.C. ; “Game Theory of Social Distancing in Response to an Epidemic” ; PLoS Comput Biol, 6 (5) : e1000793, doi:10.1371/journal.pcbi.100079, (2010).
Rhee I. et al ; “On the Levy-walk Nature of Human Mobility” : Do Humans Walk like Monkeys ?”; publié dans IEEE/ACM Transactions on Networking ; (2008)
Roberts M. et al ; “Nine challenges for deterministic epidemic models” ; Epidemics, 10, 49-53, (2015).
Sanches R.P., Massad E. ; “A comparative analysis of three different methods for the estimation of the R0 of dengue” ; Infectious Disease Modelling, 1, 88-100, (2016)
Shaman J. et al ; “Real-Time Influenza Forecasts during the 2012-2013 Season” ; Nat Commun. 4 : 2837 ; (2013).
Singh M. et al ; “Behavior Model Calibration for Epidemic Simulations” ; Proceedings of AAMAS 2018, July 10-15, 2018, Stockholm, Sweden ; (2018)
Sukumar S.R. et Nutaro J.J. ; “Agent-Based vs. Equation-based Epidemiological Models ; Proc. Conférence internationale ASE/IEEE sur l’informatique biomédicale ; (2012)
van den Driessche P. ; “Reproduction numbers of infectious disease models” ; Infectious Disease Modelling, 2, 288-303, (2017)
Wang L. et Li X. ; “Spatial epidemiology of networked metapopulation : An overview” ; Chinese Science Bulletin 59 (28), 3511-3522, (2014).
Wang Z. et al. ; “Coupled disease behaviour dynamics on complex networks” : A review” ; Physics of Life Reviews 15, 1-29 ; (2015)
Willem L. et al ; “Lessons from a decade of individual-based models for infectious disease transmission : a systematic review” ; BMC Infectious Diseases,17:612 ; (2017)
Organisation mondiale de la santé ; “Managing epidemics – Key facts about major deadly diseases” ; (2018).
Zheng Q et autres ; “Agenda driven mobility modelling” ; Int. J. Ad Hoc and Ubiquitous Computing, Vol. 5, No. 1, (2010)

