NOTA : les données utilisées proviennent du site coronavirus.politologue.com
Bref rappel sur la modélisation
Modéliser, c’est proposer une représentation de la réalité, afin de simuler le comportement d’un système. Les résultats d’un modèle, aussi pertinent soit-il, ne constitueront donc qu’une approximation de la vérité. On peut schématiquement identifier trois catégories de modèles : les modèles empiriques, analytiques et numériques :
- Les modèles empiriques ne cherchent pas à décrire la physique sous-jacente d’un phénomène, mais visent à donner une expression mathématique décrivant aussi bien que possible des résultats ou observables existants,
- Dans une approche analytique, le modélisateur établit des équations pertinentes (c’est-à-dire ayant un sens vis-à-vis du phénomène étudié) et cherche à les résoudre, au prix d’approximations et d’hypothèses maîtrisées, et en visant un temps de calcul réduit,
- Quand le système d’équation est trop complexe à résoudre directement, ou que l’on ne souhaite pas procéder à des approximations réductrices, l’utilisation d’une approche numérique s’impose. Celle-ci requiert alors l’utilisation de solveurs (techniques de résolution) spécifiques.
Les modèles empiriques nécessitent un jeu de données expérimentales conséquent, mais une puissance de calcul faible. Leur extrapolation hors du domaine de calage n’est pas légitime. À l’opposé, les modèles (ou codes) numériques, en particulier multi-dimensionnels, peuvent demander des ressources de calcul très importantes mais sont souvent utilisables ab initio et pour un champ d’application vaste (la mécanique des fluides, la thermique, etc.).
Ce qui précède est extrêmement simplifié (on pourrait souligner par exemple que les modèles numériques reposent eux-mêmes sur des sous-modèles empiriques ou analytiques : équations d’état, lois de comportement rhéologique, etc.), mais va nous permettre de mieux comprendre certaines caractéristiques des modèles épidémiologiques.
Notre premier modèle empirique
Si l’on regarde l’évolution du nombre de cas COVID-19 identifiés en France, la représentation empirique la plus adéquate présente une forme exponentielle, qui peut s’exprimer par :
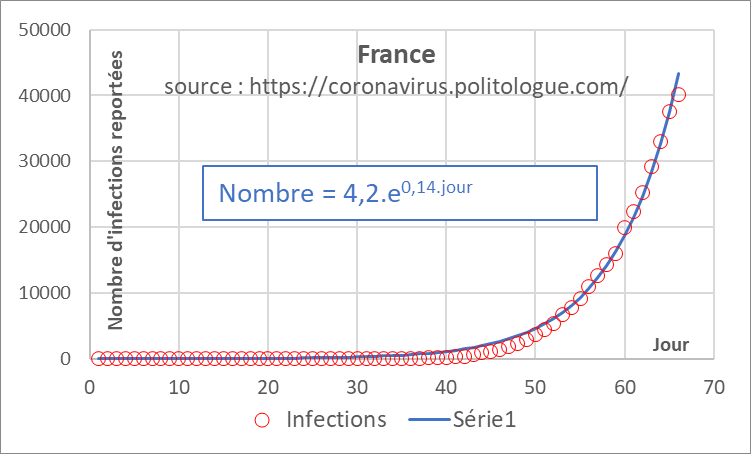
Les limites de cette représentation sont évidentes, en particulier le fait que le nombre de cas tend rapidement vers l’infini alors que la population française est d’environ 67 millions d’individus (nombre atteint au jour 118.5 environ, vers le 20 mai). Son intérêt prédictif est très limité : on ne peut pas décrire a priori l’effet de mesures visant à endiguer l’épidémie. Enfin, et même si la représentation semble adéquate, les paramètres utilisés n’ont pas de sens physique apparent.
Epidémiologie mathématique
Les modèles épidémiologiques les plus simples sont les modèles (analytiques) « à compartiments », dans lesquels la population est divisée en groupes représentant le développement de l’épidémie. Un des modèles les plus simples est le modèle à trois compartiments SIR (Susceptible, Infected, Recovered) sur lequel nous reviendrons en détails dans un prochain article, et qui permet d’ailleurs de retrouver l’évolution exponentielle du nombre de personnes infectées en début d’épidémie.
Les modèles à compartiments reposent sur l’hypothèse d’une population homogène (pas de dimension spatiale) et sont généralement résolus de manière déterministe. Leur description mathématique repose sur un jeu d’équations différentielles ordinaires (EDOs) qui décrivent les flux entre compartiments. Ces modèles comportent peu de paramètres et la charge de calcul est très faible. Cependant, leur utilisation est plus fréquemment rétrospective (pour expliquer des épidémies déjà terminées) que prédictive, car de nombreux phénomènes (mobilité, comportement humain, contre-mesures médicales et non, médicales…) ne peuvent être pris en compte. De plus, la nature intrinsèquement stochastique du problème rend délicate l’estimation des paramètres durant le cours d’une épidémie.
Pour pallier ces problèmes, de nombreuses variantes des modèles à compartiments ont été proposées : prise en compte de nouveaux compartiments, de la mobilité, de méta-populations, de réseaux de contacts ; résolution stochastique, etc. Ces modifications augmentent inévitablement le nombre de paramètres à caler…
À l’autre extrémité du spectre de complexité on trouve les modèles à base d’agents, qui peuvent être assimilés à des modèles numériques d’épidémiologie. Les « agents » représentent des individus ou des groupes d’individus ayant des caractéristiques similaires. Cette approche permet de prendre en compte des comportements complexes (catégories de personnes, mobilités réalistes, taux de contact variable en fonction du temps, influence de l’âge, etc.). En contrepartie de cette finesse de représentation, les approches à base d’agents nécessitent d’identifier dizaines ou des centaines de paramètres, et le temps de calcul est élevé (des heures, voire des jours).
À propos de la mobilité…
La modélisation des mobilités est un sous-problème important (et sous-estimé) de l’épidémiologie mathématique. La situation actuelle montre pourtant une forte hétérogénéité spatiale (cf. carte ci-dessous issue de https://coronavirus.politologue.com/carte-de-france/), et les données de téléphonique mobile arrivent à retracer par exemple la « fuite » de plus d’un million de personnes de l’Ile de France vers la province entre le 13 et le 20 mars (https://www.lemonde.fr/pixels/article/2020/03/26/confinement-plus-d-un-million-de-franciliens-ont-quitte-la-region-parisienne-en-une-semaine_6034568_4408996.html).

À l’échelle mondiale, le transport aérien a été un vecteur essentiel d’importation du Coronavirus depuis la Chine, et le sera vraisemblablement lors de futures émergences. Pour illustrer la difficulté de toute prévision, les chercheurs de l’INSERM (Institut national de la santé et de la recherche médicale) estimaient le 24 janvier en utilisant le modèle GLEAM (Global epidemic and mobility model, https://www.gleamviz.org/) que le risque d’importation par voie aérienne de l’épidémie en France était de 5% à 13%, estimation modifiée par la suite le 30 janvier. Au même moment, on pensait « très peu probable » qu’une épidémie de grande ampleur se développe en France…
Si je cite cela, ce n’est pas pour jeter la pierre à ces chercheurs, qui ont eu le courage publier de premières prévisions, mais pour montrer, en étant moi-même modélisateur, que la modélisation des phénomènes complexes est loin d’être une science exacte. Comme Cicéron, reprenant Caton, le disait déjà : « Deux augures ne peuvent se regarder sans rire… ».
De même que pour l’épidémiologie mathématique, les modèles de mobilité humaine varient du plus simple (pas de mobilité) au plus complexe (là encore, des modèles à base d’agents, tels qu’utilisés par exemple pour étudier des évacuations à l’échelle d’une ville dans le projet ANR ESCAPE – Eric Daudé). Des modèles intermédiaires empiriques peuvent être basés sur les données téléphoniques (difficiles à extrapoler d’une zone à l’autre) ou sur des relations mathématiques simples mais ayant prouvé leur efficacité (par exemple, selon la distribution de Lévy, la probabilité d’un déplacement de longueur l est proportionnelle à 1/l²).
Des recherches prometteuses sont en cours pour « donner du sens » aux modèles de déplacement, par exemple la détermination de « routines quotidiennes » (amener les enfants à l’école, aller au travail, etc.) et pourraient encore être améliorés par la prise en compte de points d’intérêts géolocalisés réels et par l’exploitation d’enquêtes statistiques (par exemple les enquêtes mobilités certifiées CEREMA, ou EMC² : https://www.cerema.fr/fr/activites/mobilite-transport/connaissance-modelisation-evaluation-mobilite/observation-analyse-mobilite/enquetes-mobilite-emc2, ou l’enquête mobilité des personnes de l’INSEE : https://www.insee.fr/fr/information/3365007).
Last but not least : le comportement humain
Les informations quotidiennes nous montrent que le comportement individuel ou de groupe joue un rôle majeur : « rush » vers les denrées essentielles lors de l’annonce du confinement, fuite des zones supposées à risques élevés, mépris par certains des consignes de confinement, etc. Ces comportements dépendent de plus fortement du pays, comme le montre par exemple une étude récente sur la vaccination (https://wellcome.ac.uk/reports/wellcome-global-monitor/2018): en France, pays le plus sceptique, 19% des personnes interrogées pensent que les vaccins ne sont pas efficaces et 33% qu’ils ne sont pas sûrs ; les chiffres respectifs en Allemagne étant 3% et 13% seulement.
Les modèles de comportement se divisent en deux grandes catégories : les modèles à base de règles et les modèles coût/bénéfice. Comme leur nom l’indique, les premiers modélisent les comportements humains par une série de règles déterministes ou stochastiques. Les seconds, dérivés de la théorie des jeux, postulent que le comportement humain vise à maximiser une fonction d’utilité (ou de gain) dont l’expression peut être très complexe. Un Ingénieur Général de l’Armement qui donnait des cours à l’ENSIETA parlait de « minimiser sa fonction d’emmerdement », ce qui revient bien sûr au même… La difficulté des modèles basés sur la théorie des jeux est le paramétrage de la fonction d’utilité, et notamment le chiffrage des « coûts » non économiques (le « coût » lié à la diminution de nos relations sociales, le « coût » d’être infecté par le coronavirus, etc.).
Il faut également mentionner que le comportement humain est influencé par les informations positives ou négatives présentes sur les différents réseaux de communication. La propagation de « fake news » ou « infox » peut d’ailleurs être modélisée par des modèles épidémiologiques…
Pour aller plus loin
Comme on peut s’en douter, les ressources sur les modèles épidémiologie mathématique ne manquent pas ces temps-ci. Quelques articles scientifiques sont proposés ci-dessous, mais ils ne constituent qu’une infime partie des informations accessibles.
Je poursuivrai d’ici quelques jours cette série par un article plus détaillé sur le modèle à compartiments SIR, mais pour l’instant je retourne au télétravail ! D’ici là restez chez vous, prenez soin de vous et de vos proches, venez en aide aux plus démunis, et ne sous-estimez pas la gravité de la situation…
Références
Allen L.J.S.; “A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis”; Infect. Disease Model., 2, 128-142; (2017).
Area Y. et al.; “On a fractional order Ebola epidemic model”; Advances in Diff. Equations, 2015:278 (2015).
Arino J. and van den Diessche P.; “Disease Spread in Metapopulations”; Fields Institute Communication; (2006).
Balcan D. et al., “Multiscale mobility networks and the spatial spreading of infectious diseases”; PNAS December 22, 2009 106 (51), 21484-21489; (2009).
Bichara D. ; « Étude de modèles épidémiologiques : Stabilité, observation et estimation de paramètres. » ; PhD dissertation ; Université de Lorraine ; (2013)
Bilge, A.H., Samanlioglu, F. & Ergonul, O.; “On the uniqueness of epidemic models fitting a normalized curve of removed individuals”; J. Math. Biol. 71, 767–794 (2015)
Brauer F. ; “Mathematical epidemiology: Past, present, and future”; Infectious Disease Modelling, 2, 113-127; (2017)
Castillo-Chavez C. et al.; “Perspectives on the role of mobility, behavior, and time-scales in the spread of diseases”; Proc Natl Acad. Sci USA, 113 (51), 14582-14588, (2016).
Chowell G.; “The basic reproduction number R0 and effectiveness of reactive interventions during dengue epidemics”; Math. Biosciences and Eng., 10 (5&6), 1455-1474, (2013)
Colizza V. et al.; “The role of the airline transportation network in the prediction and predictability of global epidemics”; PNAS February 14, 2006, 103 (7), 2015–2020; (2006)
Cooley P. et al.; “The Role of Subway Travel in an Influenza Epidemic: A NYC Simulation”; J. of Urban Health: Bulletin of the NY Academy of Medicine, Vol. 88, No. 5; (2011)
Daudé E., Eliot E. ; « Exploration de l’effet des types de mobilités sur la diffusion des épidemies » ; Septièmes Rencontres de Théo Quant, (2005).
Enduri M.K. and Jolad S.; “Dynamics of Dengue with Human and Vector Mobility”; Quantitative Biology – Polulation an d Evolution; arXiv:1409.0965 [q-bio.PE]; (2015)
European Commission; “Comparable time use statistics – National tables for 10 European countries”; ISBN 92-894-8553-1; (2005)
Favro K. and Favro-Sabatier F. ; « Comment limiter le risque infectieux du personnel médical ? » ; Revue générale de droit médical, n°16, p.135 ; (2005).
Favro K. and Zolynski C. ; « De la régulation des contenus haineux à la régulation des contenus (illicites) » ; à paraître, Légipresse.
Finger F. et al.;“Mobile phone data highlights the role of mass gatherings in the spreading of cholera outbreaks”; Proc Natl Acad. Sci USA, 113 (23), 6421-6426; (2016)
González M., Hidalgo C.A. and Barabási A.-L.; “Understanding individual human mobility patterns”; Nature 453, 779–782; (2008)
Hunter E. et al.; “A Comparison of Agent-Based and Equation Based Models for Infectious Disease Epidemiology “; in Proc. of the Irish Conf. on AI and Cognitive Science; (2018)
Kermack W.O. and McKendrick A.G.; “A contribution to the Mathematical Theory of Epidemics”; Proc. R. Soc. Lond. A, 115 ; pp. 700-721; (1927)
Maneerat S., Daudé E.; “A spatial agent-based simulation model of the dengue vector to explore its population dynamics in urban areas”; Ecological Modelling, 333, 66–78, (2016).
Mi Ondo J.M. ; « Les aspects spatiaux dans la modélisation en épidémiologie » ; PhD dissertation ; Médecine humaine et pathologie ; Université de Grenoble ; (2012).
Osthus D. et al.; “Forecasting seasonal influenza with a state-space SIR model”; Ann Appl Stat. 2017 March ; 11(1): 202–224, (2017)
Reluga T.C.; “Game Theory of Social Distancing in Response to an Epidemic”; PLoS Comput Biol, 6 (5): e1000793, doi:10.1371/journal.pcbi.100079, (2010).
Rhee I. et al.; “On the Levy-walk Nature of Human Mobility: Do Humans Walk like Monkeys?”; Published in IEEE/ACM Transactions on Networking; (2008)
Roberts M. et al.; “Nine challenges for deterministic epidemic models”; Epidemics, 10, 49-53, (2015).
Sanches R.P., Massad E.; “A comparative analysis of three different methods for the estimation of the R0 of dengue”; Infectious Disease Modelling, 1, 88-100, (2016)
Shaman J. et al.; “Real-Time Influenza Forecasts during the 2012–2013 Season”; Nat Commun. ; 4: 2837; (2013).
Singh M. et al.;“Behavior Model Calibration for Epidemic Simulations”; Proceedings of AAMAS 2018, July 10-15, 2018, Stockholm, Sweden; (2018)
Sukumar S.R. and Nutaro J.J.; “Agent-Based vs. Equation-based Epidemiological Models; Proc. ASE/IEEE International Conference on BioMedical Computing; (2012)
van den Driessche P.; “Reproduction numbers of infectious disease models”; Infectious Disease Modelling, 2, 288-303, (2017)
Wang L. and Li X.; “Spatial epidemiology of networked metapopulation: An overview”; Chinese Science Bulletin 59 (28), 3511-3522, (2014).
Wang Z. et al.; “Coupled disease–behavior dynamics on complex networks: A review”; Physics of Life Reviews 15, 1–29; (2015).
Willem L. et al.; “Lessons from a decade of individual-based models for infectious disease transmission: a systematic review”; BMC Infectious Diseases,17:612; (2017)
World Health Organization; “Managing epidemics – Key facts about major deadly diseases”; (2018).
Zheng Q et al.; “Agenda driven mobility modelling”; Int. J. Ad Hoc and Ubiquitous Computing, Vol. 5, No. 1, (2010)

