S, E, I, R, H, Q, V, D… et les autres
Comme je l’ai mentionné dans l’article précédent, les modèles épidémiologiques les plus simples sont les modèles « à compartiments », dans lesquels la population est divisée en groupes représentatifs du développement de l’épidémie. L’origine de ces modèles remonte au début du XXe siècle, l’article de référence généralement cité étant (Kermack & McKendrick, 1927), même si cet article est en fait beaucoup plus général…
Le concept de « compartiment » se comprend aisément quand on le rapproche des statistiques quotidiennes sur la pandémie COVID-19 : nombre de cas, de décès, de guérisons, et de manière plus détaillée (par exemple sur geodes.santepubliquefrance.fr) : nombre d’hospitalisations, d’admissions en réanimation… Cette catégorisation correspond aux étapes schématiques de développement de l’état de santé des patients, et donc aux « compartiments » utilisés dans les modèles simplifiés.
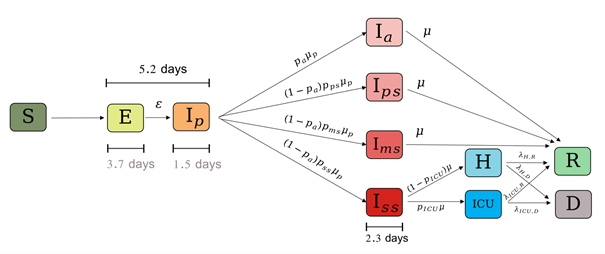
Les compartiments sont généralement identifiés par des lettres, dont le regroupement donne le nom du modèle. Un des modèles les plus simples est le modèle SIR : en anglais, ce sont les initiales de Susceptible, Infected et Recovered ou Removed (selon que l’on considère ou non la possibilité de décès). Le nombre et le type de compartiments dépendent de l’épidémie à modéliser et du niveau de détails souhaité. L’INSERM (Di Domenico & al., 2020) utilise par exemple pour le COVID-19 un modèle à trois classes d’âges et 11 compartiments, pour la plupart des sous-classes du compartiment I (voir figure ci-dessous).
Présentation du modèle SIR
« Croissance exponentielle », « aplatir la courbe », «pic épidémique », « immunité collective » ou encore « nombre (ou taux) de reproduction »… Ces expressions fréquemment entendues ou lues dans les médias font implicitement référence aux modèles épidémiologiques à compartiments. Pour savoir ce qu’elles signifient, il est indispensable de passer par la mise en équation d’un modèle, et le modèle SIR est suffisamment simple pour comprendre la logique des phénomènes étudiés. Je vais poser le modèle directement en donnant quelques explications « avec les mains » et en laissant de côté les détails mathématiques sordides, puis je discuterai des implications de cette approche en les mettant en relation avec l’actualité.
L’image qui suit montre les trois compartiments utilisés (S pour Sains ou Susceptibles, I pour Infectés et R pour Remis ou Rétablis, on ne considère pas de décès pour l’instant), les équations d’évolution pour les proportions des effectifs des compartiments notées [S], [I] et [R], et les résultats d’une simulation typique. Nous notons que dans ce modèle les individus R sont immunisés et ne peuvent donc pas être infectés à nouveau.
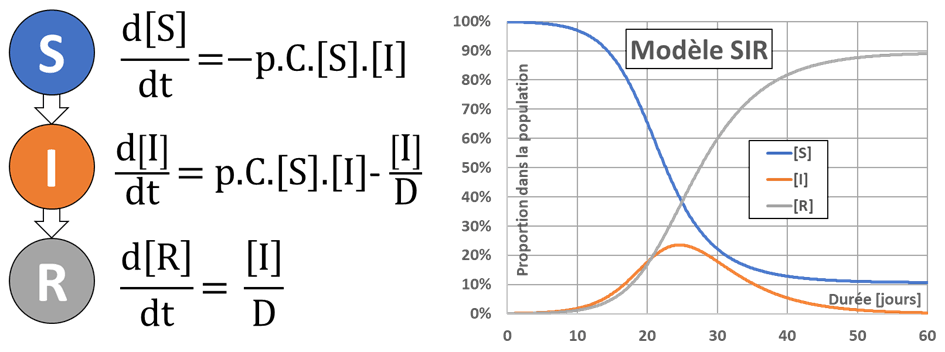
Évolution des effectifs des compartiments
Proportion d’individus sains [S]
La proportion [S] d’individus sains ne fait que diminuer. La vitesse de diminution est le produit du nombre de contacts quotidien total entre individus sains et infectés C.[S].[I] par la probabilité p qu’un contact résulte en une transmission de l’infection ; C étant le nombre moyen de contacts quotidiens par individu. Pour limiter la contamination, on peut donc chercher à diminuer p, C, ou éventuellement [I].
Quarantaine préventive : Le « stade 1 » de gestion d’une épidémie a pour but de freiner l’introduction de la maladie infectieuse sur le territoire national. On cherche à diminuer [I] (fermeture des frontières, identification des chaînes de transmission et mise en quarantaine des personnes infectées ou revenant d’une zone à risque…).
Gestes-barrière : Le port d’un masque et de gants, le lavage fréquent des mains, le respect d’une distance de sécurité, la mise en place d’écrans de protection… Toutes ces mesures visent à diminuer la probabilité p d’être infecté lors d’un contact, et contribuent ainsi à freiner la propagation de l’épidémie.
Distanciation sociale : Le « stade 2 » a pour but de freiner la propagation d’une épidémie sur le territoire national. Pour cela, des actions visant à diminuer le nombre de contacts quotidiens C sont mises en place : fermeture des écoles, des restaurants, et plus généralement des ERP (établissements recevant du public), limitation des transports, arrêt des visites aux personnes les plus vulnérables… et pour finir confinement général de la population.
Proportion d’individus guéris, ou « remis » [R]
La proportion [R] d’individus remis ne fait que qu’augmenter, par guérison progressive des personnes du compartiment I. L’équation d’évolution est construite à partir de la durée moyenne avant guérison D, et on estime que la proportion de personnes guéries chaque jour est donnée par [I]/D. Cette hypothèse simplificatrice (qui équivaut à dire que la durée de guérison suit une loi de probabilité exponentielle), généralement passée sous silence, est pourtant lourde de conséquences car cette loi de probabilité n’est pas adaptée au problème. Elle s’inscrit par contre facilement dans la mise en équation du modèle SIR (pragmatisme du modélisateur !).
Nombre de reproduction de base : le produit p.C.D correspond au nombre total de contaminations que peut provoquer un individu infecté durant tout le temps de son infection (produit du nombre quotidien de contacts C par le nombre de jours à l’état infectieux D et par la probabilité de transmettre l’infection lors d’un contact p). C’est le fameux « R0 » ou « nombre de reproduction de base », dont on entend beaucoup parler. Ce nombre de base dépend du pays (pyramide des âges…), de la notion culturelle de proxémie (Marret, 2020), des habitudes sociales (se faire la bise, se serrer la main…), etc.
Proportion d’individus infectés [I]
La proportion d’individus infectés à un instant donné varie en fonction des deux proportions précédentes, puisque [I]=1-[S]-[R] d’après l’hypothèse de population constante. Les deux contributions à cette évolution sont antagonistes : d’une part [I] va croître par contamination des personnes saines (passage S->I) et d’autre part elle va décroître par guérison des personnes infectées (passage I->R).
Pic épidémique : au début d’une épidémie [S] vaut environ 1, et le signe de d[I]/dt est donné par celui de (p.C.D–1), soit encore R0-1. Si R0 est supérieur à un, chaque personne infectée a le temps d’en infecter plus d’une lors de sa période infectieuse, l’épidémie va se propager (effet boule de neige), et on observe un pic épidémique. Dans le cas contraire, l’épidémie s’éteint d’elle-même (figure ci-dessous – pour une meilleure lisibilité le taux initial d’infectés est fixé à 10%). Plus le R0 sera grand, plus le pic épidémique (maximum de [I]) va être élevé.
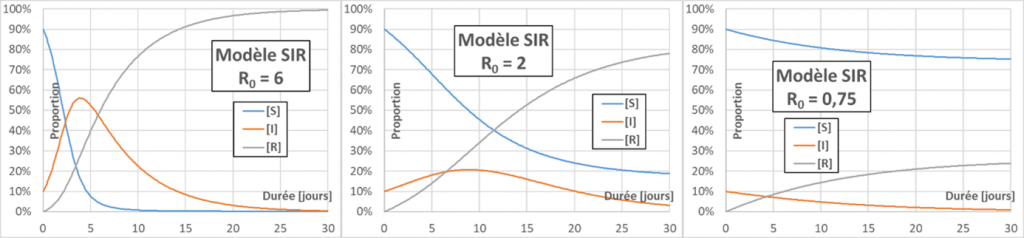
Croissance exponentielle : Dans les premiers temps de l’épidémie, nous avons vu que [S]~1. La relation d’évolution de [I] est alors de la forme d[I]/dt=k.[I]. Cette relation s’intègre facilement pour obtenir explicitement [I]=[I]0.exp(k.t), où [I]0 est la fraction initiale de population infectée et exp est la fonction exponentielle. Si R0>1, k est positif et l’évolution de [I] aux temps courts présente donc une « croissance exponentielle ».
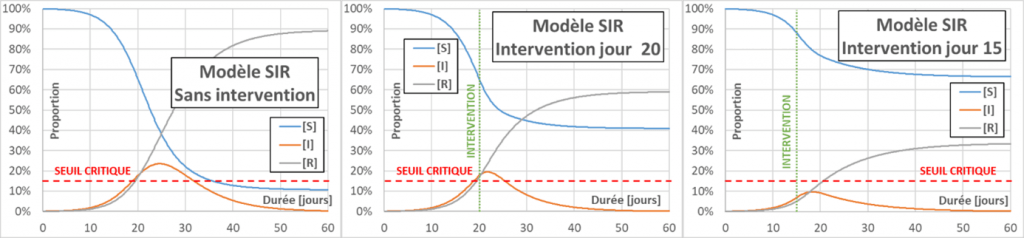
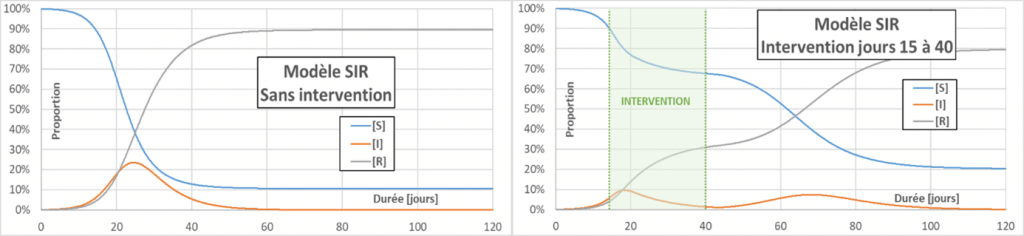
Aplatir la courbe : Les actions visant à diminuer p, C ou D (pour ce dernier, par un traitement médicamenteux par exemple) vont faire décroître le nombre de reproduction effectif Reff (contrairement à ce que l’on entend souvent – même dans la bouche d’un ministre – le R0 ne change pas). Quand Reff diminue, la courbe d’infection s’aplatit, le pic d’infection est moins grand et le nombre total de personnes infectées diminue aussi. L’intérêt principal d’aplatir la courbe est de limiter les cas grave, pour éviter de saturer les services d’urgence. Dans la figure qui suit, on compare un cas de référence (sans intervention) avec deux cas visant à diminuer Reff à une valeur de 0,75. Dans un cas l’intervention se passe au jour 20, et dans l’autre au jour 15. La figure montre également un seuil critique (fictif) de saturation des services d’urgence. On constate l’intérêt de prendre de mesures très précoces.
Immunité collective : Le nombre de reproduction effectif Reff diminue aussi, dans le courant d’une épidémie, avec la proportion de personnes saines [S]. Si on ne change rien à p, C et D, quand une épidémie peut-elle décroître « naturellement » ? Le signe de (p.C.[S]-1/ D) nous donne une nouvelle fois la réponse : L’épidémie va décroître quand [S] devient inférieure à 1/R0. À ce moment, la proportion de personnes ayant été infectées est la somme de [I] (celles qui sont encore infectées) et [R] (celles qui sont guéries). Comme [S]+[I]+[R]=1, le critère d’arrêt précédent se traduit aussi par [I]+[R]>1–1/R0. C’est « l’immunité collective », qui se comprend facilement : le risque de contact entre personnes saines et personnes infectées diminue quand il reste très peu de personnes saines ; les nombreuses personnes guéries faisant « tampon » entre les deux autres catégories.
Deuxième vague : Le confinement ne prétend pas résoudre le problème d’une épidémie, mais gagner du temps sur le développement de vaccins et de traitements ainsi que sur l’adaptation des lieux de travail, et bien sûr de ne pas surcharger les services d’urgence en « aplatissant la courbe ». Lorsque le confinement est relâché, de nouveaux cas vont apparaître, comme le montre la figure ci-dessous : c’est la « deuxième vague ». Outre la diminution des pics épidémiques par rapport à une situation sans intervention, on observe également au final une plus grande proportion d’individus n’ayant jamais été infectés.
Stop-and-go : Dernier slogan médiatique en date, le “stop-and-go” désigne une stratégie de gestion de l’épidémie basée sur l’alternance entre périodes de confinement et périodes de reprise d’activité, afin de multiplier les « petits pics » et d’étaler dans le temps la survenue de nouveaux cas. Comme pour le confinement simple, il s’agit essentiellement de gagner du temps par rapport à l’élaboration des vaccins et traitements, en essayant de maintenir à flot l’activité économique du pays.
Réflexions générales sur le modèle et ses résultats
Limites des modèles à compartiment
La première limite des modèles à compartiments est l’homogénéité de la population étudiée et des contacts iner-individus. Dans ces modèles, un individu a la même probabilité de rencontrer n’importe quel autre individu de la population, mais nos contacts ne se passent pas de cette manière : nous créons des relations privilégiées – et donc de possibles contacts – au travers de réseaux multiples (notre voisinage, notre travail, les associations auxquelles nous participons, les commerces que nous fréquentons…) et non de manière indifférenciée. Par ailleurs, le nombre moyen de contacts varie fortement entre les individus (selon l’âge, le tempérament…), mais aussi selon les périodes de l’année ou encore par la participation à certains évènements exceptionnels (assister à un match de football, être invité à un mariage, etc.). Des approches plus fines font appel à des « matrices de contact » associées à des probabilités variées de transmission. Ces probabilités de transmission ne sont d’ailleurs pas constantes et devraient, pour une personne infectée, évoluer au fil du temps (la notion de « charge virale » pourrait par exemple être utilisée).
La deuxième limite est l’absence de dimension spatiale. Ce qui est flagrant dans une épidémie, c’est la présence de « foyers infectieux » (ou « clusters ») géographiquement localisés, qui vont induire un développement très différent de l’épidémie selon les pays, les régions ou les villes. Dans les modèles à compartiments, chaque individu peut être en contact avec n’importe quel autre, sans notion de distance ou de densité locale de population ce qui n’est bien sûr pas le cas dans la vie « réelle ». La prise en compte d’une dimension spatiale peut se faire de bien des manières, mais n’est pas évidente à intégrer dans un modèle à compartiments. L’article (Yeghikyan, 2020) illustre bien ces deux premiers points.
La troisième limite est une prise en compte bancale de la dimension temporelle. Nous avons vu que la représentation de la durée avant guérison n’était pas adaptée. Toutes les phases temporelles des modèles à compartiments plus complexes (durée entre réanimation et décès, entre infection et consultation, entre début d’un traitement et guérison, entre contamination et début de transmission, etc.) sont représentées de la même manière. Des solutions plus appropriées existent, mais sont beaucoup plus complexes à mettre en œuvre : on peut par exemple utiliser des fonctions « à retard », en formalisant par exemple pour le modèle SIR un lien entre [R](t) et [I](t-d), d suivant une loi de probabilité plus adéquate.
La quatrième limite est le caractère déterministe de la résolution. Une simulation partant des mêmes conditions de départ aboutira forcément au même résultat, et les incertitudes sur ces résultats n’apparaîtront pas clairement, donnant l’impression que les résultats du modèle présentent un caractère de vérité absolue. Il est cependant assez facile de passer à une résolution stochastique en faisant varier les paramètres et les conditions initiales et en lançant plusieurs centaines de simulations au lieu d’une simulation unique (approche type Monte-Carlo). Au lieu de courbes bien définies, on verra apparaître une courbe moyenne entourée d’une zone de variation probable, par exemple un intervalle de confiance à 95%. Dans certains cas, cette zone d’incertitude est tellement grande que le modèle n’a plus d’intérêt pratique… L’article (Gonçalves, 2020) traite notamment de ce point, et comme pour le précédent les codes Python sont fournis pour pouvoir reproduire les résultats et tester des variantes.
Les difficultés du paramétrage
Le modèle SIR ne comprend que deux paramètres : le produit p.C (que l’on peut éventuellement individualiser) et la durée D. Malheureusement, une épidémie n’arrive pas avec sa carte d’identité, et les valeurs de ses paramètres caractéristiques doivent être trouvées par traitement des données observables de propagation de l’épidémie.
De quoi disposons-nous pour le COVID-19 ? Une bonne connaissance de la courbe d’évolution de [I] nous donnerait au moins R0-1, mais la comptabilité officielle exclut de facto les cas asymptomatiques ou pauci-symptomatiques, puisque ces cas ne conduisent ni à une hospitalisation, ni à une consultation chez le médecin. Par ailleurs, le mode même de décompte varie en fonction du temps : pour la France, les données initiales provenaient des hôpitaux uniquement, puis on a ajouté les données partielles (décès essentiellement) provenant des EHPAD, et ensuite les données de médecine de ville (consultations avec un tableau symptomatique évoquant le COVID-19), au risque de comptabiliser aussi les cas « canada-dry » d’autres affections pulmonaires : ça ressemble au COVID, ça a les symptômes du COVID, mais ce n’est pas le COVID…
Vous l’avez compris, on ne peut pas non plus se fier aux données sur les décès, pour les mêmes raisons que précédemment (sans compter que le taux de mortalité dépend de bien d’autres paramètres, et qu’il est donc difficile de remonter à [I]…). Des informations récentes laissent penser que plusieurs milliers de décès à domicile sont également dus au COVID et n’ont pas été comptabilisées… l’INSEE commence à exploiter les informations de surmortalité par rapport aux années précédentes, mais le traitement statistique associé est extrêmement complexe car la cause du décès n’est pas indiquée, et la surmortalité liée au COVID est partiellement compensée par d’autres phénomènes, comme la baisse des accidents de la circulation, entre autres.
La seule manière de connaître réellement la proportion de personnes touchées par le COVID-19 est de procéder à des tests à très grande échelle afin de mieux appréhender également les niveaux de réponse des individus à l’infection. Le taux de décès des personnes infectées pourrait être également mieux connu, puisqu’on ramènerait les décès observés au nombre total d’infections et non aux seules infections ayant entraîné une hospitalisation.
Mais du coup, à quoi ça sert ?
Il est clair que le modèle SIR et ses différentes variantes sont trop simples pour prévoir avec une fiabilité correcte le devenir de l’infection. Ajouter des paramètres et des compartiments amplifie les difficultés liées au paramétrage, et un modèle aussi simple ne peut pas être meilleur que les données qui le supportent, données dont le recueil est trop incertain pour servir de référence absolue. La variabilité des paramètres publiés pour le COVID-19 dans la littérature illustre d’ailleurs la complexité du problème…
Si un tel modèle ne peut être calé qu’à la fin d’une épidémie (ou en révisant périodiquement les valeurs des paramètres pour les faire coller au mieux avec les données observées), et s’il n’a donc aucune valeur prédictive, à quoi tout cela peut-il bien servir ?
Ces modèles permettent tout d’abord de comparer qualitativement des scénarios : que se passerait-il si on réduisait notablement les contacts (de 25%, de 50%…), si on prolongeait la période de confinement de 10 jours ou d’un mois, etc. Cela pourrait aussi permettre de communiquer vers la population sur l’intérêt des gestes barrière, de la distanciation sociale, etc., même s’il faut au préalable arriver à « vulgariser » certaines notions. Ce n’est pas une bien grande réussite à mon avis pour l’instant, et nous sommes essentiellement soumis à la comptabilité anxiogène des nouveaux cas et des décès, sans tentative de contextualisation et d’explication, sans parler de nombreuses informations peu fiables et contradictoires…
En conclusion : comment une épidémie peut-elle s’arrêter ?
Finalement, c’est quand même le plus important : comment cela peut-il finir ?
Immunité collective – une fausse bonne idée : En considérant les hypothèses optimistes d’une immunité acquise après infection (nous y reviendrons), d’un R0 valant 2 et d’un taux de mortalité pour les personnes infectées égal à 0,5%, le seuil d’immunité au COVID-19 serait atteint lorsque 50% au moins de la population aurait attrapé le virus. Pour la population française (67 millions de personnes), cela conduirait à plus de 167 000 décès. Avec des hypothèses moins optimistes (R0=2,5 ; 1% de mortalité) on dépasserait facilement les 400 000 morts, et bien plus encore en cas de saturation des services d’urgence (car le taux de mortalité serait bien supérieur). Donc non, clairement l’immunité collective n’est pas une solution !
Vaccination : Pour simplifier, la vaccination revient à passer directement du compartiment S au compartiment R, sans transiter par la phase « maladie » (ce qui permet d’éviter les décès). Le taux de vaccination minimal efficace est donc le même que le seuil d’immunité collective, à savoir 1–1/R0. La vaccination, si elle est possible, serait par contre une solution efficace contre le COVID-19.
Rémission spontanée : Par analogie avec le virus de la grippe, et parce que les coronavirus connus semblent également sensibles à l’exposition à l’air sec, certains scientifiques estiment que l’épidémie pourrait s’éteindre d’elle-même à l’été (il y a quelques semaines, on entendait « au printemps »). Cela ne veut pas dire que la pandémie cesserait définitivement, mais qu’elle pourrait prendre un caractère saisonnier, ou bien s’enraciner de manière endémique sur nos territoires. En clair, nous vivrons encore longtemps avec…
Et si l’immunité n’est pas acquise ?
Une infection conduit l’organisme à générer des anticorps (leur détection est le principe de fonctionnement des tests sérologiques). On peut espérer que les personnes séropositives au Coronavirus soient définitivement immunisées contre celui-ci (compartiment R), mais ce n’est absolument pas une certitude… L’immunité dépend-elle du niveau initial de l’infection ? Est-elle de longue durée ? Serait-elle valable contre des mutations du virus ? La communauté scientifique est pour l’instant incapable de répondre à ces questions cruciales.
Dans le pire des cas, s’il n’y a aucune immunité, le modèle SIR se réduit en un modèle SI : le compartiment S se comporte alors comme le tonneau percé des Danaïdes : Au fur et à mesure que le compartiment se remplit par « retour » des individus infectés I en individus susceptibles S (et non plus « sains » dans ce cas), il se vide au travers de nouvelles infections qui transforment les individus S en I… Inutile de préciser dans ce cas que tout le monde finirait par attraper la maladie (et même plusieurs fois au fil des années)…
Ce doute sur l’immunité face au COVID interroge aussi sur la possibilité de développer un vaccin totalement efficace. À la difficulté initiale (aucun vaccin n’ayant été développé jusque là pour un coronavirus) s’ajoute donc une incertitude sur la faisabilité même d’un vaccin ainsi que des interrogations sur les mutations possibles du COVID-19, qui induiraient un travail permanent d’adaptation du vaccin (comme Sisyphe et son rocher, pour changer de métaphore mythologique). Un vaccin, même imparfait, qui limiterait la possibilité de développer des formes graves de la maladie, serait déjà une très bonne nouvelle… qui n’est pas attendue avant (au mieux) mi-2021.
D’ici là, on peut espérer au moins le développement de traitements qui, administrés suffisamment tôt, diminueraient le risque de décès en cas de maladie… On compte donc beaucoup sur les chercheurs, et bien sûr et toujours sur les soignants, un grand merci à eux !
Pour aller plus loin :
Les articles et sites internet cités dans le texte sont repris en référence ci-dessous. Je signale aussi l’excellent site https://www.3blue1brown.com/ et sa chaîne YouTube, qui présente des vidéos de vulgarisation scientifique extrêmement bien réalisées, y compris pour des domaines très complexes (l’auteur met même à disposition le code Python qui permet de créer ses propres animations). Concernant notre sujet, je vous conseille vivement les vidéos « Exponential Growth and Epidemics » et surtout « Simulating an epidemic », dans laquelle les thèmes que j’ai abordés trouvent une illustration très originale.
Di Domenico L., Pullano G., Sabbatini C.E., Boëlle P.-Y., Colizza V. ; Expected impact of lockdown in Île-de-France and possible exit strategies; Report #9; www.epicx-lab.com/covid-19.html.
Gonçalves B., Article medium, 2020 : https://medium.com/data-for-science/epidemic-modeling-101-or-why-your-covid19-exponential-fits-are-wrong-97aa50c55f8
Kermack W.O. and McKendrick A.G.; “A contribution to the Mathematical Theory of Epidemics”; Proc. R. Soc. Lond. A, 115 ; pp. 700-721; (1927).
Marret J.-L.; COVID-19 : la distance sociale (confinement et proximité : une approche par les sciences sociales) ; Note n°09/20, Fondation pour la Recherche Stratégique.
Yeghikyan G., Article towardsdatascience, 2020 : https://towardsdatascience.com/modelling-the-coronavirus-epidemic-spreading-in-a-city-with-python-babd14d82fa2

